 |
|
Neubewertung des Michelson-Morley Experiments |
||
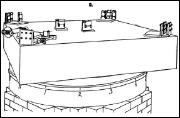 Michelson-Morley Interferometer |
Ein wesentlicher Unterschied zwischen der Äther-Hypothese und der speziellen Relativitätstheorie liegt in der Definition der Lichtgeschwindigkeit. Beim Äther-Ansatz können je nach Betrachterstandpunkt von c abweichende Werte (in Bewegungsrichtung c-v und entgegen der Bewegungsrichtung c+v) auftreten. Und genau diesen Geschwindigkeitsunterschied wollten die Forscher Michelson und Morley bei ihrem denkwürdigen Experiment nachweisen. Dabei sollten Interferenzänderungen eine Reduktion der Lichtgeschwindigkeit in Bewegungsrichtung der Erde nachweisen. Der Versuch scheiterte. Es wurde der Gedanke des Äthers als Lichtmedium aufgegeben und durch Einsteins spezielle Relativitätstheorie (SRT) ersetzt. |
|
Eingangsbedingungen |
||
Bei der Lorentz-Transformation und den von Einstein verwendeten Formeln wird lediglich zwischen den Originalwerten (l und t) und den transformierten Werten (l' und t') unterschieden. Dies führt immer wieder zu Verwechslungen und Berechnungsfehlern. |
||
Berechnung der Wellenmaxima in Bewegungsrichtung |
||
Sollte es ein absolut ruhendes Bezugssystem geben, so muss sich ein Lichtstrahl gegenüber einem bewegten System, je nach Bewegungsrichtung um die Geschwindigkeit v schneller, bzw. langsamer ausbreiten. Dies bedeutet, dass ein Lichtstrahl in Bewegungsrichtung längere Zeit benötigt um die Strecke l zu überbrücken. Analog dazu müssen sich die Geschwindigkeiten von Licht und bewegtem System in Gegenrichtung addieren, die Laufzeit des Strahls verkürzt sich entsprechend. Für beide Richtungen benötigt der Lichtstrahl in einem bewegten System immer etwas länger als in einem ruhenden System. Ist dies jedoch der Fall, so muss die gemessene Lichtgeschwindigkeit gegenüber dem ruhenden System abweichen und es ist zu erwarten, dass die Symmetrie des Lichtstrahls gestört ist, was zu einer Verschiebung der Wellenmaxima und somit zu einer Veränderung der Interferenzmuster führt. (mathematische Herleitung [152 KB] ) |
||
Einfluss von Längenkontraktion und Zeitdilatation |
||
Wie eingangs schon gezeigt, besteht jedoch kein Zweifel an der Gültigkeit der Zeitdilatation und der Längenkontraktion. Betrachten wir daher den Versuch aus relativistischer Sicht unter Einbeziehung aller gemessener Werte die wir auf ein ruhendes Bezugssystem transformieren. Zunächst müssen wir also die Verkürzung der Strecke l in Bewegungsrichtung gemäß der Formel für die Längenkontraktion berücksichtigen. Zudem müssen alle gemessenen Zeiten mit dem Gamma-Faktor für die Zeitdilatation korrigiert werden. Doch obwohl die Längenkontraktion und die Zeitdilatation in die Berechnung für den Michelson-Morley-Versuch eingeflossen sind, ergibt sich für die Anzahl der Wellenmaxima immer noch eine geringe Abweichung, die mit heutigen Versuchen auf jeden Fall nachgewiesen werden könnte. Es muss also noch einen Faktor geben, der bei der Korrektur zu berücksichtigen ist. (mathematische Herleitung [165 KB] ) |
||
Zeitdilatation der Frequenz |
||
Bei genauerer Untersuchung stellt sich heraus, dass ein zeitabhängiger Faktor noch nicht kompensiert wurde, nämlich die Frequenz. D.h. in dem durch die Zeitdilatation verlangsamten System erscheint die Frequenz wie im Zeitraffer höher als aus Sicht eines ruhenden Beobachters. Es handelt sich hierbei nicht um den optischen Dopplereffekt, der dann auftritt, wenn sich eine Lichtquelle auf einen Betrachter zu oder von ihm weg bewegt. Im Fall des Michelson-Morley Experiments bewegen sich Lichtquelle und Betrachter mit der gleichen Geschwindigkeit, es tritt also kein optischer Dopplereffekt auf. Dennoch muss die Frequenz f als inverse Funktion der Zeit berücksichtigt, und auch auf sie der inverse Gamma-Faktor für die Zeitdilatation angewandt werden. Dieser Effekt wird auch als transversaler Dopplereffekt bezeichnet (mehr dazu...). Nun kürzen sich die beiden Kompensationsfaktoren und somit die Relativgeschwindigkeit heraus. Das bedeutet, egal wie schnell sich ein Inertialsystem bewegt, es wird in Bewegungsrichtung immer die gleiche Anzahl an Wellenmaxima wie im ruhenden Zustand zu messen sein. (mathematische Herleitung [150 KB] ) |
||
Beispiel: Wellenmaxima in Bewegungsrichtung |
||
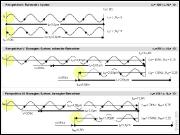 Zum Vergrößern bitte anklicken |
Im nebenstehenden Beispiel wird ein Lichtstrahl zwischen zwei Spiegeln im Abstand von 3,0µm reflektiert. Im ruhenden System durchläuft der Lichtstrahl 10 Wellenmaxima, pro Richtung jeweils 5 Maxima. Wird das System nun mit 35% der Lichtgeschwindigkeit linear bewegt, so verschiebt sich die Anzahl der Maxima. In Bewegungsrichtung sind es nun 7 und entgegen der Bewegungsrichtung 3. Der Grund ist der, dass der Lichtstrahl in Bewegungsrichtung hinter dem Spiegel hereilt und somit einen längeren Weg überbrücken muss, entgegen der Bewegungsrichtung kommt ihm der erste Spiegel entgegen und verkürzt somit den Weg. Aufgrund der Zeitdilatation erscheint dem bewegten Beobachter die Lichtfrequenz höher als dem ruhenden Beobachter, das schlägt sich in der dargestellten Länge der beiden Wellenzüge nieder. Somit erhält der bewegte Beobachter auch für die Geschwindigkeitsmessung des Lichtstrahls in beide Richtungen den Wert von 100% c. Der unbewegte Beobachter ermittelt jedoch nur 88% c gegenüber dem bewegten System. Die genaue Berechnung zu diesem Beispiel kann hier als Excel-Datei heruntergeladen werden. |
|
Wellenmaxima senkrecht zur Bewegungsrichtung |
||
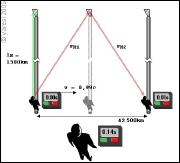
|
Nun gilt es jedoch auch zu untersuchen, wie sich bei dieser Transformation die Wellenmaxima senkrecht zur Bewegungsrichtung verhalten. Denn auch hierfür muss gelten, dass die Anzahl der Wellenmaxima konstant ist. Da senkrecht zur Bewegungsrichtung keine Längenkontraktion auftritt, ist zunächst anzunehmen, dass zur Berechnung der Wellenmaxima alle Ruhewerte genutzt werden können. Da jedoch die Zeitdilatation für alle Richtungen gilt, muss sie sowohl auf die Laufzeiten, als auch auf die Emissionsfrequenz angewandt werden. Unter diesen Bedingungen zeigt sich, dass die Anzahl der Frequenzmaxima deutlich von den Werten parallel zur Bewegungsrichtung abweichen. Dieses Ergebnis ist überraschend, da sich eigentlich der senkrecht zur Bewegung laufende Lichtstrahl so verhalten sollte, wie im ruhenden System. Doch bei genauer Betrachtung stellt sich heraus, dass dem nicht so ist. |
|
Auswirkungen auf das Michelson-Morley Experiment |
||
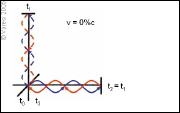
|
In diesem Beispiel treten im ruhenden System sowohl am Längs- als auch am Querarm des Michelson-Morley Interferometers zwei komplette Wellenzüge auf, in Hin- und Rückrichtung sind das je Arm vier Wellenzüge. Dabei sind folgende Zeitpunkte wichtig: zum Zeitpunkt t0 wird der Strahl in Quer- und Längsrichtung aufgespaltet, nach genau der halben Zeit (Zeitpunkt t1) wird der Strahl am Ende des Querarms reflektiert, zum Zeitpunkt t2 wird der Strahl am Ende des Längsarms reflektiert, wobei t2 = t1 nur für das ruhende System gilt und zum Zeitpunkt t3 treffen beide Strahlengänge auf dem Beobachtungsschirm zusammen und werden zur Interferenz gebracht. (Grafik vergrößern ) |
|

|
In einem System, das mit 25% c bewegt wird, ist die Wellenlänge aufgrund der Zeitdilatation so stark gedehnt, dass trotz längerem Weg entlang des Querarms je Richtung weiterhin nur 2 Wellenmaxima auftreten. Entlang des Längsarms, der aufgrund der Längenkontraktion verkürzt ist, tritt ebenfalls die Dehnung der Wellenlänge auf. Da sich das System unter dem Lichtstrahl wegbewegt, muss er in Bewegungsrichtung 2,5 statt lediglich zwei Wellenzüge durchlaufen. Entgegen der Bewegungsrichtung addiert sich die Bewegungsgeschwindigkeit zur Lichtgeschwindigkeit, so dass der Lichtstrahl nur 1,5 Wellenzüge benötigt, um am Beobachtungsschirm anzukommen. In Summe benötigt der Lichtstrahl in beide Richtungen wie im ruhenden System nur vier Wellenzüge. (Grafik vergrößern ) |
|
|
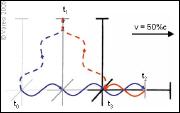
In einem System, das mit 50% c bewegt wird, wird die Wellenlänge aufgrund der Zeitdilatation noch stärker gedehnt, so dass am Querarm je Richtung weiterhin nur zwei Wellenzüge benötigt werden. Am Längsarm benötigt der Lichtstrahl nun drei komplette Wellenzüge um den Spiegel zu erreichen. In Gegenrichtung erreicht er bereits nach einem Wellenzug den Beobachtungsschirm. Auch in diesem Fall werden in Summe weiterhin nur vier Wellenzüge benötigt. Egal wie schnell sich das System bewegt, das Verhältnis der Wellenzüge in beide Richtungen ist aufgrund Zeitdilatation, Längenkontraktion und transversalem Dopplereffekt stets konstant. (Grafik vergrößern ) |
|
Fazit |
||
Mit den bisherigen Transformationen konnte eindeutig gezeigt werden, dass aus Sicht eines unbewegten Betrachters unabhängig von der Bewegungsgeschwindigkeit immer die gleiche Anzahl an Wellenmaxima gemessen werden muss. Doch wie steht es um die Anzahl an Wellenmaxima aus Sicht des bewegten Systems? Vergleichen wir einfach die Anzahl der errechneten Wellenmaxima mit den Schlaglöchern einer Straße. Es ist dabei gleichgültig, von welchem Betrachterstandpunkt aus beobachtet wird, über wie viele Schlaglöcher ein Auto rast. Sowohl der unbewegte Beobachter als auch der bewegte Beobachter werden die gleiche Anzahl an Schlaglöchern bzw. Wellenmaxima zählen. |
||
 © Andreas Varesi 6.2005-2006
/
Stand: 8.1.2006
/
Besucher |